Der Ausgleich von Beobachtungswerten

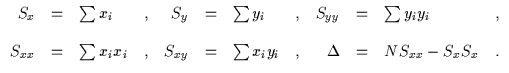
Die Ausgleichung von Beobachtungen nach der Methode der kleinsten Quadrate ist weitestgehend üblich und bekannt. Die dazu erforderlichen Rechnungen finden sich allgegenwärtig in der mathematischen Literatur und sind auch häufig schon im Lieferumfang gehoben ausgestatteter Taschenrechner oder aber auch von Tabellenkalkulationsprogrammen enthalten. Etwas diffiziler wird die Sache aber, wenn spätestens zur Veröffentlichung der erhaltenen neuen Erkenntnisse nach den Fehlern der Koeffizienten gesucht wird. Im linearen Fall hilft auch hier (fast) jedes mathematische Nachschlagewerk; wenn aber, wie im Fall von Bedeckungssternen mit wechselwirkenden Komponenten, eine ausgleichende quadratische Parabel gefunden werden soll, endet die praktische Hilfe in der einschlägigen Literatur bestenfalls mit dem Hinweis auf das zugrundeliegende Gleichungssystem und das Fehlerfortpflanzungsgesetz. Bei der Auswertung von Beobachtungen an V366 Cas (siehe dazu IBVS 4798 = BAVM 116) stellte sich uns dieses Problem nun aber in recht drängender Form, so daß sich einer der Autoren (PK) den Mühen der Herleitung unterziehen mußte. Damit die Ergebnisse dieser doch etwas aufwendigen Beschäftigung auch denen, die sich mit ähnlichen Problemen konfrontiert sehen, als Kochrezept , d.h. ohne detaillierte Herleitung, zur Verfügung stehen, haben wir uns entschlossen, den nachfolgenden Beitrag zu schreiben.

Für die erhaltenen N Meßwertpaare (x_i,y_i), i=1...N, das könnten z.B. die Epochenzahlen ( als x_i ) und (B-R)-Werte ( als y_i ) von Minima oder Maxima veränderlicher Sterne sein, soll zunächst ein linearer Ansatz

y_i=ax_i+b

gemacht werden, damit, um im obigen Beispiel zu bleiben, die bisher veröffentlichten Elemente mit den gefundenen Werten für a (Periode) bzw. b (Nullepoche) verbessert werden können. Zur Vereinfachung der nachfolgenden Rechnungen werden nun folgende Definitionen getroffen (die Summen laufen dabei jeweils über alle i=1, ..., N ):

Damit errechnen sich am Ende die Koeffizienten zu

$$a=\frac{1}{\Delta }\left( NS_{xy}-S_{x}S_{y}\left) \right. \right.$$

$$b=\frac{1}{\Delta }\left( S_{xx}S_{y}-S_{xy}S_{x}\left) \right. \right.$$

und die zugehörigen Fehler sind dann

$$\sigma _{a}^{2}=\sigma ^{2}\enspace \frac{N}{\Delta }$$

$$\sigma _{b}^{2}=\sigma ^{2}\enspace \frac{S_{xx}}{\Delta }$$

worin die Standardabweichung der Einzelwerte mit

$$\sigma^{2} =\frac{1}{N-2}\left( a^{2}S_{xx}+2abS_{x}-2aS_{xy}-2bS_{y}+S_{yy}+b^{2}N\right)$$

enthalten ist.

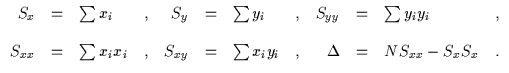
Ganz ähnlich geht man für einen quadratischen Ansatz

y_i=ax_i²+bx_i+c

vor, indem man wiederum zunächst zur Vereinfachung definiert:

$\Delta = S_{xxxx}(NS_{xx}-S_{x}S_{x})+S_{xxx}(S_{x}S_{xx}-NS_{xxx})+S_{xx}(S_{xxx}S_{x}-S_{xx}S_{xx})$

Die Koeffizienten des Ansatzes erhält man dann zu

$$a=\frac{1}{\Delta }\left[ S_{xxy}\left( NS_{xx}-S_{x}S_{x}\ri... ...S_{xx}\left( S_{xy}S_{x}-S_{xx}S_{y}\right) \right] \hskip 2mm,$$

$$b=\frac{1}{\Delta }\left[ S_{xxxx}\left( NS_{xy}-S_{x}S_{y}\r... ...{xx}\left( S_{xxx}S_{y}-S_{xy}S_{xx}\right) \right]\hskip 2mm,$$

$$c=\frac{1}{\Delta }\left[ S_{xxxx}\left( S_{xx}S_{y}-S_{xy}S_... ...xxy}\left( S_{xxx}S_{x}-S_{xx}S_{xx}\right) \right]\hskip 2mm.$$

wobei für deren Fehler die Beziehungen

$$\sigma _{a}^{2}=\sigma ^{2}\enspace \frac{1}{\Delta }\left( NS_{xx}-S_{x}S_{x}\right)\hskip 2mm,$$

$$\sigma _{b}^{2}=\sigma ^{2}\enspace \frac{1}{\Delta }\left( NS_{xxxx}-S_{xx}S_{xx}\right) \hskip 2mm,$$

$$\sigma _{c}^{2}=\sigma ^{2}\enspace \frac{1}{\Delta }\left( S_{xxxx}S_{xx}-S_{xxx}S_{xxx}\right)$$

gelten, worin wiederum die Standardabweichung der Einzelwerte mit

$$\sigma ^{2}=\frac{1}{N-3}\left[ a^{2}S_{xxxx}+2abS_{xxx}+\lef... ..._{xx}+2bcS_{x}-2aS_{xxy}-2bS_{xy}-2cS_{y}+S_{yy}+c^{2}N\right]$$

enthalten ist.

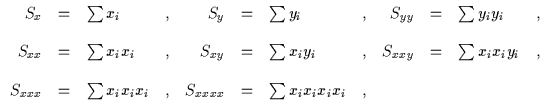
Ein Beispiel

Vorab noch ein Hinweis für jene, die die obigen Gleichungen in ein kleines Rechnerprogramm packen wollen: Es wird hier gleichzeitig mit sehr großen und sehr kleinen Zahlen gerechnet; für die zugehörigen Variablen sind daher entsprechend passende Typen (double =8-Byte-Zahl) zu wählen, um dann auch mit der nötigen Präzision rechnen zu können. Als Übungsaufgabe sollen die beobachteten und in den BAV Mitteilungen 116 veröffentlichten Minima von V366 Cas dienen; wer die in der dortigen Tabelle 1 enthaltenen Daten mit den nachstehenden Elementen (Berthold, 1978, Hartha Mitt. 12.2 = Elemente (1) im IBVS) reduziert, sollte die (B-R)-Werte aus dem dort in der Abbildung 1 gezeigten Diagramm erhalten.

$${\rm JD}(min,hel) = 2435075.461 + 0\fday72927425 \times E$$

Achtung: Vor weiteren Rechnungen ist zu bedenken, daß die oben aufgeführten Bestimmungsgleichungen nur für Beobachtungen bzw. Messungen mit gleichem Gewicht gelten. In unserem Beispiel, welches Daten unterschiedlicher Genauigkeit enthält, muß deshalb bei der Berechnung der Summen jeder Datensatz seinem Gewicht W entsprechend W-fach verwendet werden! Ein quadratischer Fit (mit den Epochenzahlen als unabhängiger Variabler!) liefert dann für die Koeffizienten bzw. ihre Fehler:

Dankenswerterweise sind nun die Koeffizienten schon mit den passenden Vorzeichen versehen, so daß nur noch addiert werden muß, um die Gleichung für die ausgleichende Parabel und damit die entsprechend verbesserten Elemente zu erhalten:

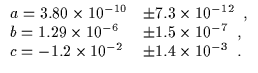
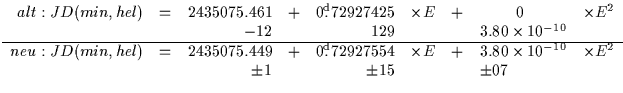
Wem das zu einfach ist, der kann natürlich auch die Ausgleichnung unter Verwendung des Julianischen Datums als unabhängiger Variabler durchführen. Die dabei erhaltenen Koeffizienten, hier zur Unterscheidung A,B und C genannt, müssen dann erst noch entsprechend umgerechnet werden. Zwischen dem Julianischem Datum JD eines beobachteten Ereignisses und der zugehörigen Epoche E besteht bekanntermaßen der Zusammenhang

wobei E₀ die Ausgangsepoche und P die Periode ist. Umformen dieser Gleichung und einsetzen in die Bestimmungsgleichung der Parabel liefert die folgenden Rekursionsgleichungen:

Mit den zugehörigen Fehlern ist in gleicher Weise zu verfahren. Dann sind die Koeffizienten a,b und c wie oben gezeigt anzuwenden, um die parabolischen Elemente zu erhalten.

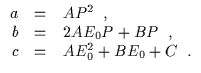
THOMAS BERTHOLD		PETER KROLL
Bruno-H.-Bürgel-Sternwarte Hartha		Sternwarte Sonneberg
e-mail: berthold.mtl@t-online.de		e-mail: pk@stw.tu-ilmenau.de